"Man is the measure of all things" – Protagoras (Greek Sophist, 485-411 B.C.)
History of measurement
The beginnings
Until the 18th century there was no unified measurement system. In spite of the attempts of Charlemagne and many kings after him, aiming to reduce the number of existing measurements, France was one of the most inventive and most chaotic countries in this area. In 1795 there were over seven hundred different "unit of measurement" in France.
Many were simply borrowed from human morphology. Their names often referred to parts of the body: the digit, the hand, the foot, the cubit, the pace, the fathom or toise, whose Latin name tensa - from brachia - the distance across a man's outstretched arms. These units of measure were not fixed: they varied from one town to another, from one occupation to another, as well on the type of object to be measured. Floor area was measured in square feet, for example, and carpet area in square ells.
Volume and length measurements were totally unrelated. For each unit of measure, the multiples and sub-multiples were fixed randomly, making calculations extremely laborious. To understand the difficulties resulting from such systems, we must consider the modern way of measuring time, a survivor of the old system of subdivisions. In this system, all calculations involve prior conversion.
A source of error and fraud in commercial transactions, this situation also put a check on the development of science. With the expansion of industry and trade, there was an increasing need for harmonisation.
A universal measure : the metre
Politicians and scientists did their best to remedy this situation. Their intention was to produce an invariable measure by comparison with a standard borrowed from a natural phenomenon, the universal standard that Condorcet had dreamed of as far back as 1775, which would not be based on any national vanity and which could be used by all foreign nations.
The climate of reform which followed the revolution precipitated the choice of a standard. The lists of grievances claimed this universal measure to do away with the arbitrary seigneurial measurements.
On 16 February 1791, following a proposal by the Chevalier JC de Borda - the inventor of the pendulum and the "Borda repeating circle" - a commission was set up to bring in a uniform system of measurement. The commission, composed of Borda, Condorcet, Laplace, Lagrange and Monge was faced with a choice between three possible references: the length of a simple pendulum beating at a rate of one second at a latitude of 45°, the length of one quarter of the equator or, lastly, the distance from the North pole to the equator, a quarter meridian.
Since the pendulum beating at a rate of one second involved time and varied at different points on the globe (the length of the pendulum would have had to be corrected according to the acceleration due to gravity), the quarter meridian therefore appeared as the simplest solution to calculate and the most universal.
Introduced on 26 March 1791, the metre was defined as being equal to the ten millionth part of one quarter of the terrestrial meridian*. The metre materialised the idea of a "unit which in its determination was neither arbitrary nor related to any particular nation on the globe".
The exact length of the meridian still had to be found, however, which turned out to be a real adventure for the geodesists in charge of the mission, Pierre-François MECHAIN (1744-1804) and Jean-Baptiste DELAMBRE (1747-1822).
These two men alone were to carry out the triangulation work which would forever link their names to this new measurement of the meridian. Lasting almost seven years, the work took them from Dunkirk to Barcelona.
Using the triangulation system, the 18th century scientists managed to determine the exact length of a quarter meridian, equivalent to ten million metres.
See the Meridian of Delambre and Méchain between Dunkirk and Barcelona
* At the time of the definition as it was defined and written, the definition of the meridian was considered to be that of astronomy: a meridian was a complete circle. So for the earth around 40 000 km, the 10 millionth of a quarter of the meridian corresponds to 1 m. Not to be confused with the definition of the geographical meridian which was established after the first definition of the metre and which is defined as a semicircle, therefore 20 000 km for the earth.
The decimal metric system, a revolutionary invention
Once the base unit of measure had been determined, all that had to be done now was "just" to establish all the other resulting units of measurement: the square metre and the cubic metre, the litre, the gram, etc.
The decimal metric system was introduced on 18 germinal year III (7 April 1795) by the law "on weights and measures". This caused a major upheaval in everyday life. Decimalisation also brought a real revolution in the calculation of areas and volumes. Conversion from a multiple to a sub-multiple unit in area, and vice versa, simply consists of moving the decimal point two places, or three places for volume.
To determine the unit of mass, the commission preferred water to any other body such as mercury or gold, due to the "ease of obtaining water and distilling it…". The kilogram was defined as being equal to the mass of a cubic decimetre of water at a given temperature.
For everyday use, the first standards of the metre and the kilogram were manufactured in 1799 and deposited in the Archives of the Republic, dedicated to "all men and all times".
Both simple and universal, the decimal metric system started to spread outside France. The development of railways, the growth of industry and the increasing number of exchanges all required accurate units of measure. Adopted at the start of the 19th century in several Italian provinces, the metric system became compulsory in the Netherlands from 1816 and was chosen by Spain in 1849.
In France, after a few contradictory measures, the decimal metric system was exclusively adopted with the law of 4 July 1837, under the Guizot ministry. It had taken almost half a century to adopt a system which had been created in the enthusiasm springing from the Revolution.
After 1860, adhesion increased particularly in the Latin American countries which joined the ranks of the many countries taking up the metric system. Nevertheless, these countries were dependent on France whenever exact copies of the metre and kilogram standards were required. This subordination to France, together with the lack of uniformity in making copies, was likely to jeopardise the desired unification. To overcome these difficulties, the Bureau International des Poids et Mesures (B.I.P.M.) was founded in 1875, during the diplomatic conference of the metre which led, on 20 May 1875 to the signature of the treaty known as the Metre Convention by the plenipotentiaries of 17 States.
The BIPM's initial mission was to set up the decimal Metric System throughout the world by constructing and maintaining new prototypes of the metre and the kilogram, comparing the national standards with these prototypes and perfecting the measurement methods in order to promote metrology in all fields.
The BIPM progressively focused on the study of metrological problems and physical constants which govern the precision of measurements when defining units (e.g. thermometry), then, to accompany industrial development, its scope extended to new fields: the electrical units (1927), the photometric units (1937), the ionising radiation measurement standards (1960) and the quantity of matter (1971).
From the metric system to the International System of Units (SI)
The International System of Units (SI), successor of the metric system, was officially founded in 1960 following a resolution made in the 11th Conférence Générale des Poids et Mesures (CGPM). All units of measurement can be reduced to a small number of fundamental standards with this system, which dedicates the necessary care to continuously improve their definition. This represents one of the missions of the national metrology laboratories.
The definitions of the SI base units have changed over the years, to meet the requirements of certain users who demanded greater precision.
The measurement methods and the standards themselves undergo constant progress and are permanently renewed; the greater the precision in the definition of the units of measure, the finer the values measured can be. The work on fundamental standards, carried out in particular by the national metrology laboratories and the Bureau International des Poids et Mesures, will probably never end.
This is reflected in the changing of the definition of the metre, away from a material object.
Although universal, the implementation of the metre unit defined as a proportion of the quarter meridian was clearly difficult to implement. This explains why its standard was first the metre stored in the Archives, the international prototype metre from 1889.
On 14 August 1960, the metre was redefined as being equal to 1 650 763,73 times the wavelength of orange radiation from the krypton 86 atom in vacuum. This definition, based on a physical phenomenon, marked the return to a natural, reproducible standard, permanent and invariable, offering an accuracy nearly fifty times greater than that of the international prototype and a better guarantee of very long term maintenance.
In 1983, following the important work on the speed of light and on atomic clocks, the metre was redefined as "the distance travelled by light in vacuum in 1/299 792 458 of a second".
*pictures extracted from the book "L'épopée du mètre" (published by the French Ministry in charge of Industry and Regional Planning)
The Metre adventure
The metre, base of the new metric system
On 19 March 1791 the metre, the base of the new metric system, was theoretically defined as being equal to the ten millionth part of one quarter of the terrestrial meridian. Practically, the length of the meridian still had to be set up, however.
In its "report on the choice of units of measurement", the Academy of Science defined the various steps that this work would involve: the length of the meridian would be determined by triangulation, from an arc of nine and a half degrees between Dunkirk and Barcelona.
Triangulation, a method known since the early 17th century
Already in 1718, Jacques Cassini used this method to measure the meridian between Dunkirk and Collioure. Triangulation consists of marking a route by a network of highly visible landmarks: tower, peak, church spire, etc., these points representing a series of connected triangles. The method involves trigonometric calculations. Knowing all the angles formed by two adjacent triangles and at least one of the lengths in one of these triangles, one can determine the lengths of all sides in both triangles.
On 13 April 1791, the Academy appointed the members of the commissions who would perform the measurements
The triangulation and determination of the latitudes were to be carried out by Jacques Cassini's son, Legendre and Méchain.
Monge and Meusnier were to measure the bases. In June 1791, Cassini simply visited with Méchain the base of Villejuif at Juvisy (the obelisk is currently known as the Pyramide de Juvisy). Although Cassini expected to be able to use this old base, which had already been used by his father in 1739, his grandfather in 1701, and Abbot Picard in 1670 when they carried out their triangulation calculations ; he was unable to do so. Cassini then stayed in Paris to help Borda. Monge and Legendre did very little in fact. Meusnier left to join the Rhine army and was killed in 1793. Delambre, who had just joined the Academy of Science was then nominated to replace them.
A precision instrument: The Borda circle
Measurement of the meridian arc involved the use of precision instruments and was partly justified by improvements to these instruments. Of much greater precision, these measurements would replace the previous ones taken fifty years before.
To determine the angles, our two geodesists were going to use the new Borda repeating circle. Using this innovation, angles could be measured to the nearest second, whereas with the quadrants used so far it had only been possible to obtain accuracy to the nearest 15 seconds. The ground measurements, in Toise du Pérou units, were to be made with copper-platinum bimetal rulers. Obviously, any other unit would have been suitable, since once the length of the quarter of the meridian* is determined, dividing it by 10 000 000 would give the length of a metre. In this case, the length of the first metre was therefore expressed in Toise du Pérou units; in 1747, La Contamine had brought back this measurement unit from his expedition to the equator, but it only became a national standard on 16 May 1766 after a royal declaration.
* At the time of the definition as it was defined and written, the definition of the meridian was considered to be that of astronomy: a meridian was a complete circle. So for the earth around 40 000 km, the 10 millionth of a quarter of the meridian corresponds to 1 m. Not to be confused with the definition of the geographical meridian which was established after the first definition of the metre and which is defined as a semicircle, therefore 20 000 km for the Earth.
Two teams for measuring the meridian arc
Delambre's team included the Frenchmen Lalande and Bellet; Tranchot and Esteveny accompanied Méchain. The Academy of Science distributed the work involved in measurement of the meridian arc as follows: the two upper thirds, from Dunkirk to Rodez, were assigned to Delambre; the last third, from Rodez to Barcelona, was assigned to Méchain. This difference could be explained by the fact that Delambre's route would theoretically follow close to the points of the former triangulation, whereas Méchain would explore territory where no geodesic measurements had yet been made.
In practice, the earlier triangulation landmarks turned out to be unusable: during the turmoil of the revolution, some spires had disappeared or were about to collapse. Peak after peak, Delambre discovered that it was impossible to use Cassini's previous landmarks: the old spires had been rebuilt differently after being burnt down.
Mark out the meridian arc: a very difficult enterprise
More than one hundred triangles were required to mark out the meridian arc; our two geodesists were to experience numerous mishaps during their expedition: arrests, temporary revocations, damaged or destroyed geodesic equipment. The marker signals they used for their observations aroused the distrust of the population; the material attached at the end of their signals was white, the colour of royalty, and therefore a counter-revolutionary colour. In spite of their passes, passports and other authorisations, our two scientists were still not safe from arrest, since the authorities which had issued these documents disappeared, making them outlaws. For instance, following the abolition of the Academies (in 1793), Delambre found that he had been excluded from the temporary commission of weights and measures (in 1794) and therefore prohibited from continuing his work, until June 1795. Méchain also experienced numerous setbacks.
Landmarks to establish, mountains to cross, not forgetting the historical events :
War broke out on 7 March 1793 between France and Spain, where some of his measurements had to be made. From 1793 to 1795 therefore, the Terror regime was to delay his triangulation calculations. At the same time, the metre was temporarily fixed by the law of 1 August 1793 according to the results of measuring the French meridian, published by Lacaille in the 1758 Mémoires de l'Académie. Moreover, the decimal subdivisions of the metre were to be the decimetre, the centimetre and the millimetre. This temporary standard metre did not correspond to the work carried out by Méchain and Delambre, but to the results of Cassini's earlier triangulation.
1799, a new platinum metre standard
In 1795, with the improvement of the political situation, the triangulation work was able to resume. It continued for a further three years, before the length of the quarter of the meridian could be accurately determined and a new platinum metre standard dedicated to "all times and all men " was deposited in 1799, in the archives of the republic.
*pictures extracted from the book "L'épopée du mètre" (published by the French Ministry in charge of Industry and Regional Planning)
The SI since May 2019
Since its adoption by the CGPM in 1960, the SI has been revised several times. However, the revision voted in 2018 and come into effect in May 2019 is exceptional in that it formally amends all the unit definitions at once, revising four of them in a fundamental way,. The scope of this revision is such that it has required numerous international collaborations between numerous metrologists and scientists in the most diverse fields of science.
2018 : paradigm shift
The 2018 revision constitutes a major evolution of the international system of units (SI), while of course preserving all the units of measurement: the same 7 basic units associated with the same 7 basic quantities; the derived units and the prefixes already listed are not modified.
However, this is a significant and fundamental evolution for scientists: the foundation on which all these units are built has been shaken. In an industrial and medical context where measurements require greater requirements (level of uncertainty, cross-referencing of data of different quantities, increasingly efficient technological means, etc.), it seems essential to make the SI even more coherent than it already is. Three major reasons can easily be given to support this argument: the variation observed over a century in the numerical value of the standard kilogram (international prototype of the kilogram - IPK); the impossibility of realizing in practice the definition of the ampere; the independence of the definitions for most of them.
The basic principle of the revision of the SI is to base it not on the units themselves as it previously was, but on 7 constants of physics: this is the paradigm shift of 2018. These constants, which will therefore be called SI definition constants, are based on physical phenomena of a fundamental, universal nature (such as h, the Planck constant) or are derived from specific properties (such as the luminous efficacy of the eye). Relying on a "fixed" data base to build the new system is therefore the guarantee of working with coherent measures whose limits can be more easily pushed back (in theory).
The values of these constants have, for four of them (Planck, Boltzmann, Avogadro, elementary charge), required a long-term work on an international scale. Metrology requires redundancy to validate such changes. Numerous experiments have been set up in order to fix the numerical values, accepted by the international community. The convergence of the results (ensured by several conditions previously defined at the launch of these studies by the Consultative Committee of the Units under the authority of the BIPM), led in July 2017 to a set of numerical values endorsed by CODATA and summarized below.
| Name | Symbol | Numerical value | Unit |
|---|---|---|---|
| Planck constant | h | 6,626 070 15 x 10-34 | J∙s |
| Elementary charge | e | 1,602 176 634 x 10-19 | C |
| Boltzmann constant | k | 1,380 649 x 10-23 | J∙K-1 |
| Avogadro constant | NA | 6,022 140 76 x 1023 | mol-1 |
French contributions
At the 21st General Conference on Weights and Measures in 1999, the following recommendation was endorsed by the member states: "... that national laboratories continue their efforts to refine experiments which link the unit of mass to fundamental or atomic constants and which could, in the future, serve as a basis for a new definition of the kilogram...".
Several national metrology institutes have thus directed their efforts towards improving the uncertainty of the value of fundamental constants and launched experiments for the realization of units, in particular for units relating to mass, electricity, temperature and amount of substance.
The French metrology network therefore started several research projects in the years following this recommendation, enabling France to be at the forefront of this new redefinition of the IS. Our national work has therefore focused on the following areas.
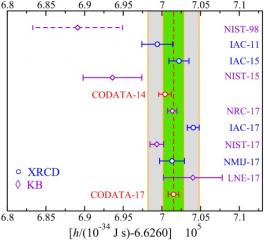
The kilogram and the Planck constant, h
The Kibble balance (formerly called the "watt balance") is an instrumentation that makes it possible to compare, in two configurations (called static and dynamic) two types of energy : one electrical, of which the elementary quantification is the Planck constant ; the other mechanical, of a potential nature and related to the mass of the object being compared.
The French teams therefore embarked in 2002 on a large-scale project to design and produce this instrumentation, involving researchers from Cnam, LNE and Paris Observatory. Each team brings its expertise in the main scientific fields of the experiment: mass, electricity and magnetism and gravimetry. The objective was initially (for the July 2017 deadline) to contribute to the international determination of the value of h with a target uncertainty of 8 x 10-8. Four h values were successively published by France between 2014 and 2017. The laboratory is now one of the international laboratories (with NRC - Canada, NIST - United States) that have contributed to the current determination of this fundamental constant, through Kibble's balance experiment. The current objective is to carry out the chain of dissemination of the kilogram in France, in accordance with the missions of our national laboratories. Work has already been carried out within the framework of the European NewKilo project to evaluate the use of several materials as potential transfer standards. More specifically, the studies focused on the surface physico-chemistry of artefacts of different compositions. Iridium seems to be a good candidate because it has low magnetic susceptibility (≃ +3.7 x 10-5) and high hardness (≃ 450 Hv).
Reference : “Data and analysis for the CODATA 2017 special fundamental constants adjustment*” Peter J Mohr, David B Newell, Barry N Taylor and Eite Tiesinga, METROLOGIA, VOLUME 55, NUMBER 1
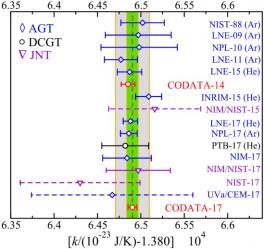
The kelvin, through the determination of the Boltzmann constant, k
Two methods have been explored by French laboratories. The spectroscopic method by the Laboratoire de Physique des Lasers and the acoustic method by the Laboratoire commun de métrologie.
The LNE-LCM published 4 Boltzmann constant values, the last of which, in 2017, is the best result obtained internationally: 1.380 648 78 J·K-1 with an uncertainty of less than 6.10-7.
Reference : “Data and analysis for the CODATA 2017 special fundamental constants adjustment*” Peter J Mohr, David B Newell, Barry N Taylor and Eite Tiesinga,
METROLOGIA, VOLUME 55,NUMBER 1
Traceability to the ampere
Until the revision of its definition in 2018, the stricto-sensus realization of the ampere was not made, its definition making it impracticable (infinite conductors, negligible sections, in vacuum,...). The realization could be done via farad, ohm and volt. The discoveries of the quantum Hall effect and the Josephson effect, respectively for resistance and voltage measurements, have revolutionized electrical metrology. Electrical standards have been implemented for many years using these quantum devices, and already based on the fundamental constants : e and h. However, the universality of these phenomena had to be proven. To make the system coherent, the LNE teams worked on this new definition by studying the direct determination of the von Klitzing constant (RK) by producing a new Thompson-Lampard calculable standard with five electrodes. These developments have demonstrated the feasibility of the operation. The development of this instrumentation continues today within the framework of the implementation of a powerful impedance comparison chain: this set will allow a direct determination of the farad, then of the ohm in SI units.
Furthermore, the new definition of ampere can be put into practice using a quantum current standard. The French teams are currently continuing their development of an electrical quantum current source (between 10 pA and 100 pA) with an accuracy of the order of 10-7 in relative value. This was also the objective of the European EMRP Qu-Ampere project, completed in April 2015 and to which LNE contributed by studying new electron pumps and developing a new cryogenic current comparator (CCC).
Perspectives for the SI
Redefinition of the second
International authorities are already considering future improvements to the SI definitions, in particular for the candela and the second. Today, the second is defined from atomic clocks with cesium atoms that operate at microwave frequencies (around 9 GHz). Scientific research has shown that the higher the frequency, the lower the measurement uncertainty on the frequency. The next step, for the realization of the unit of time, is the improvement of accuracy by very promising developments of clocks, this time in the optical frequency range (a few hundred THz), clocks with neutral atoms or ions. France, for its part, is developing two types of clocks with Sr and Hg neutral atoms. Such experiments should improve the definition of the second by more than an order of magnitude.
Digitalization of metrology
Digital transformation of metrology refers to the adoption and integration of digital technologies into measurement processes. It has significant impacts on the future of metrology, transforming the way measurements are carried out and facilitating the exchange and management of data.
We can list some of the key impacts of the digital transformation of metrology:
1. Automation of measurement processes: Digital technologies enable processes to be automated, thereby reducing reliance on human intervention and minimizing potential errors. This improves the reproducibility and accuracy of measurements, as well as increasing the efficiency of operations related to the measurement process.
2. Smart sensors and Internet of Things (IoT): Smart sensors connected in networks play a key role in the digital transformation of metrology. These sensors are capable of collecting measurement data in real time, transmitting it to central computer systems and analyzing it automatically. This allows continuous, real-time monitoring of measured quantities, thus improving the responsiveness and management of measurement processes.
3. Data analysis and machine learning: these developments in metrology tend towards the exploitation of vast quantities of measurement data generated. Data analysis and machine learning techniques can be used to extract relevant information from this data, identify patterns, detect anomalies, and improve measurement performance. This paves the way for more predictive and proactive metrology.
4. Integration of quality management systems: Digital technologies facilitate the integration of quality management systems with metrology processes. Measurement data can be directly integrated into quality management systems, strengthening traceability and quality assurance of products and services. It also allows for more efficient management of calibration certificates, reference standards and quality control procedures.
5. Interconnection and data exchange: Digital technologies facilitate the exchange and sharing of measurement data among different stakeholders, such as metrology laboratories, manufacturers, regulatory bodies, etc. This promotes collaboration, transparency and interoperability between the different players in the sector, which contributes to the overall improvement of the quality of measurements.
In summary, the digital transformation of metrology is revolutionizing traditional measurement practices by integrating advanced digital technologies. This leads to more automated, accurate, predictive and integrated metrology, with significant impacts on improving measurement quality, process productivity and decision-making based on reliable measurement data.