"L'homme est la mesure de toutes choses" - Protagoras (sophiste grec, 485-411 av. JC)
Histoire de la mesure
Les balbutiements
Jusqu'au XVIIIème siècle il n'existait aucun système de mesure unifié. Malgré les tentatives de Charlemagne et de nombreux rois après lui, visant à réduire le nombre de mesures existantes, la France comptait parmi les pays les plus inventifs et les plus chaotiques dans ce domaine. En 1795, il existait en France plus de sept cents unités de mesure différentes.
Nombre d'entre elles étaient empruntées à la morphologie humaine. Leur nom en conservait fréquemment le souvenir : le doigt, la palme, le pied, la coudée, le pas, la brasse, ou encore la toise, dont le nom latin tensa - de brachia - désigne l'étendue des bras. Ces unités de mesures n'étaient pas fixes : elles variaient d'une ville à l'autre, d'une corporation à l'autre, mais aussi selon la nature de l'objet mesuré. Ainsi, par exemple, la superficie des planchers s'exprimait en pieds carrés et celle des tapis en aunes carrées.
Les mesures de volume et celles de longueur n'avaient aucun lien entre elles. Pour chaque unité de mesure les multiples et sous multiples s'échelonnaient de façon aléatoire, ce qui rendait tout calcul extrêmement laborieux. Pour comprendre les difficultés qu'entraînaient de tels systèmes, il convient de considérer le mode actuel de la mesure du temps, survivance de l'ancien système de subdivisions. Dans ce système, tout calcul implique une conversion préalable.
Source d'erreurs et de fraudes lors des transactions commerciales, cette situation portait aussi préjudice au développement des sciences. A mesure que l'industrie et le commerce prenaient de l'ampleur, la nécessité d'une harmonisation se faisait de plus en plus pressante.
Une mesure universelle : le mètre
Politiques et scientifiques, vont tenter de réformer cet état de fait. Leur idée est d'assurer l'invariabilité des mesures en les rapportant à un étalon emprunté à un phénomène naturel, un étalon universel qui, ainsi que Condorcet le rêvait déjà en 1775, ne serait fondé sur aucune vanité nationale, permettant l'adhésion de toutes les nations étrangères.
Le climat de réforme qui suivit les événements révolutionnaires permit de précipiter le choix d'un étalon. Les cahiers de doléance réclamaient cette mesure universelle pour s'affranchir de l'arbitraire des unités de mesure seigneuriales.
Le 16 février 1791, sur la proposition Du Chevalier JC de Borda - l'inventeur du pendule et du "cercle répétiteur" qui portent son nom - une commission chargée de fixer la base de l'unité des mesures est constituée. La commission, composée de Borda, Condorcet, Laplace, Lagrange et Monge doit opérer son choix entre trois références possibles : la longueur du pendule simple à secondes à la latitude de 45°, la longueur du quart du cercle de l'équateur, ou enfin la longueur du quart du méridien terrestre.
Alors que le pendule battant la seconde présentait l'inconvénient de faire intervenir des durées, et de varier selon les points du globe (la longueur du pendule aurait du être corrigée en fonction de l'intensité de la pesanteur), le méridien apparaissait comme la solution la plus simple à calculer et la plus universelle.
Le 26 mars 1791 naissait le mètre, dont la longueur était établie comme égale à la dix millionième partie du quart du méridien* terrestre. Le mètre concrétisait l'idée d'une " unité qui dans sa détermination, ne renfermait rien ni d'arbitraire ni de particulier à la situation d'aucun peuple sur le globe ".
Mais il restait encore à établir la longueur exacte du méridien, ce qui donna lieu à une véritable épopée pour les géodésiens chargés de cette mission, Pierre-François MECHAIN (1744-1804) et Jean-Baptiste DELAMBRE (1749-1822).
A eux seuls, ces deux hommes vont se charger des opérations de triangulation qui lieront leur nom pour la postérité à cette nouvelle mesure du méridien. Ces travaux prirent près de sept ans et les conduisirent de Dunkerque à Barcelone.
C’est en utilisant le système de la triangulation que les scientifiques du 18e siècle sont parvenus à déterminer une longueur d'un quart de méridien, dont la dix millionième partie donne la valeur du mètre.
Voir la Méridienne de Delambre et Méchain entre Dunkerque et Barcelone
* A l’époque de la définition telle qu’elle a été définie et inscrite, on considérait la définition du méridien comme celle de l’astronomie : un méridien était un cercle complet. Donc pour la terre autour de 40 000 km, le 10 millionième du quart du méridien correspond à 1 m. A ne pas confondre avec la définition du méridien géographique qui a été établi après la première définition du mètre et qui est défini comme un demi-cercle, donc 20 000 km pour la terre.
Le système métrique décimal, une invention révolutionnaire
L'unité de mesure de base étant déterminée, il " suffisait " désormais d'établir toutes les autres unités de mesure qui en découlaient : le mètre carré et le mètre cube, le litre, le gramme...
Le système métrique décimal est alors institué le 18 germinal an III (7 avril 1795) par la loi " relative aux poids et mesures ". Il s'agit d'un bouleversement majeur des pratiques humaines. La décimalisation introduisait une véritable révolution dans le calcul des surfaces et des volumes. Tout passage d'une surface multiple à un sous-multiple, et vice versa, s'opère par simple glissement de la virgule décimale de deux rangs, de trois rangs s'il s'agit de volume.
Pour déterminer l'unité de masse, la commission préféra l'eau à tout autre corps tel que le mercure ou l'or, en égard à " la facilité de se procurer de l'eau et de la distiller... ". Il fut établi que le kilogramme serait égal à la masse d'un décimètre cube d'eau à une température donnée.
Pour l'usage courant, les premiers étalons du mètre et du kilogramme furent fabriqués en 1799 et déposés aux Archives de la République, dédiés "à tous les hommes et à tous les temps".
Le système métrique décimal à la fois simple et universel commence à se propager hors de France. Le développement des réseaux ferroviaires, l'essor de l'industrie, la multiplication des échanges exigent des mesures précises. Adopté dès le début du 19e siècle dans plusieurs provinces italiennes, le système métrique est rendu obligatoire aux Pays Bas dès 1816 et choisi par l'Espagne en 1849.
En France, après quelques mesures contradictoires, la loi du 4 juillet 1837, sous le ministère de Guizot, permet l'adoption exclusive du système métrique décimal. Il aura fallu près d'un demi-siècle pour aboutir à l'adoption d'un système créé pourtant dans l'enthousiasme sous la Révolution.
Après 1860 les adhésions se multiplient gagnant les pays d'Amérique Latine, et un nombre conséquent de pays, l'ont déjà adopté. Néanmoins, ces pays sont dépendants de la France chaque fois qu'il s'agit d'obtenir des copies exactes des étalons du mètre et du kilogramme. Cette subordination à la France, ajoutée au manque d'uniformité dans l'établissement des copies, risque de compromettre l'unification souhaitée. Pour palier ces difficultés le Bureau international des poids et mesures (BIPM) voit le jour en 1875, lors d’une conférence internationale diplomatique ; cette dernière aboutit, le 20 mai 1875 à la signature par les plénipotentiaires de 17 Etats du traité connu sous le nom de Convention du mètre.
La mission initiale du BIPM était d'assurer l'établissement du Système Métrique décimal dans le monde entier par la construction et la conservation des nouveaux prototypes du mètre et du kilogramme, de comparer les étalons nationaux à ces prototypes, et de perfectionner les procédés de mesure afin de favoriser les progrès de la métrologie dans tous les domaines.
Néanmoins, le BIPM s'est progressivement orienté vers l'étude des problèmes métrologiques et des constantes physiques qui conditionnent l’exactitude des mesures lors de la définition des unités (tel que la thermométrie par exemple), puis au fil des développements industriels, ses attributions ont été étendues à de nouveaux domaines : les unités électriques (1927), photométriques (1937) ou les étalons de mesure pour les rayonnements ionisants (1960) et la quantité de matière (1971).
Du système métrique au Système international d'unités (SI)
Le Système international d'unité (SI), successeur du système métrique, est officiellement né en 1960 à partir d'une résolution de la 11ème Conférence générale des poids et mesures. Ce système permet de rapporter toutes les unités de mesure à un petit nombre d'étalons fondamentaux, et de consacrer tous les soins nécessaires à améliorer sans cesse leur définition. C'est là, une des missions des différents laboratoires nationaux de métrologie.
Les définitions des unités de base du SI ont évolué au cours de l'histoire dès que les besoins de précision de certains utilisateurs n'étaient plus satisfaits.
Les méthodes de mesure et les étalons eux-mêmes progressent et se renouvellent constamment ; en effet, plus les unités de mesure ont une définition précise, et plus les valeurs mesurées peuvent être fines. Les travaux concernant les étalons fondamentaux, effectués notamment par les laboratoires nationaux de métrologie du LNE et par le Bureau international des poids et mesures, ne connaîtront sans doute jamais de fin.
L'évolution de la définition du mètre dans le sens de sa dématérialisation en est l'illustration.
L'unité mètre définie par rapport au quart du méridien, avait un caractère universel mais il est certain que sa mise en oeuvre soulevait de nombreuses difficultés. C'est pourquoi son étalon fut d'abord le mètre des Archives, puis le prototype international du mètre à partir de 1889.
Le 14 août 1960, le mètre est redéfini comme étant égal à 1 650 763,73 fois la longueur d'onde, dans le vide, d'une radiation orangée de l'atome krypton 86. Cette définition, fondée sur un phénomène physique, marquait le retour à un étalon naturel, reproductible, offrant des garanties de permanence et d'invariabilité permettant d'avoir une exactitude près de cinquante fois supérieure à celle qu'autorisait le prototype international, et une meilleure garantie de conservation à très long terme.
En 1983, suite aux importants travaux sur la vitesse de la lumière et sur les horloges atomiques, le mètre est redéfini en fonction de la vitesse de la lumière, comme égal " à la longueur du trajet parcouru dans le vide par la lumière pendant 1/299 792 458 de seconde ".
*photos extraites de l'ouvrage "L'épopée du mètre" (par Louis MARQUET et Albert LE BOUCH, publié par le ministère de l'industrie et de l'aménagement du territoire)
Épopée du mètre
Le mètre, base du nouveau système métrique
Dès le 19 mars 1791 le mètre, base du nouveau système métrique, était théoriquement défini comme égal à la dix millionième partie du quart du méridien terrestre, encore fallait-il établir dans la pratique la longueur de ce dernier.
L’académie des sciences définissait, dans son "rapport sur le choix des unités de mesure", les différentes étapes que ces travaux devaient suivre : la longueur du méridien serait déterminée à partir d’un arc de 9 degré et demi entre Dunkerque et Barcelone, la méthode employée serait la triangulation.
La triangulation, une méthode connue depuis le début du XVIIe siècle
En 1718, déjà, elle avait permis à Jacques Cassini de réaliser sa mesure du méridien entre Dunkerque et Collioure. La triangulation consiste à jalonner un itinéraire par un réseau de points que l’on choisit pour leur visibilité : tour, sommet, clocher... Ces points devant former des triangles juxtaposés. Cette méthode fait appel à des calculs de trigonométrie et permet, si l’on connaît tous les angles formés par deux triangles adjacents et au moins une des longueurs d’un seul de ces deux triangles, de déterminer la grandeur de tous les côtés de deux triangles.
Le 13 avril 1791, l’académie désigne les membres des commissions devant effectuer les opérations de mesure
La triangulation et la détermination des latitudes sont confiées à Cassini ( le fils de Jacques Cassini), Legendre et Méchain.
La mesure des bases doit être effectuée par Monge et Meusnier. En juin 1791, Cassini se contente de visiter avec Méchain la base entre Villejuif et Juvisy en région parisienne (l’obélisque est connu actuellement sous le nom de Pyramide de Juvisy). Cassini pense pouvoir réutiliser cette ancienne base qui déjà avait servi à son père en 1739, à son grand-père en 1701, et à L’abbé Picard en 1670 pour chacune de leur triangulation, mais il n’en sera rien. Cassini restera ensuite à Paris pour aider Borda. Monge et Legendre ne feront presque rien. Meusnier, quant à lui, partira pour l’armée du Rhin et se fera tuer en 1793. Delambre, qui venait d’entrer à l’Académie des Sciences est alors désigné pour les remplacer.
Un instrument de précision : le cercle Borda
La mesure de l’arc du méridien nécessitait l’utilisation d’instruments de précision et se justifiait en partie par leurs améliorations, leur nouvelle précision rendait caduque les anciennes mesures effectuées cinquante ans auparavant.
En effet, pour la détermination des angles, nos deux géodésiens allaient utiliser le nouveau cercle répétiteur de Borda. Cette innovation permettait désormais d’obtenir des angles à la seconde près, alors que les quarts de cercle que l’on utilisait jusqu’alors ne donnaient des angles qu’à 15 secondes près. Les mesures au sol seraient faites avec des règles bimétalliques cuivre-platine dont l’unité serait la toise du Pérou. Bien entendu n’importe quelle autre unité aurait fait l’affaire, puisque une fois déterminée la longueur du quart du méridien*, la division de celle-ci par 10 000 000, donnerait la longueur d’un mètre. Pour le cas présent, la longueur du premier mètre serait donc exprimée en toise du Pérou ; en 1747, La Contamine avait rapporté cette unité de mesure de son expédition en équateur, mais celle-ci n’était devenue un étalon national que le 16 mai 1766 après une Déclaration du roi.
* A l’époque de la définition telle qu’elle a été définie et inscrite, on considérait la définition du méridien comme celle de l’astronomie : un méridien était un cercle complet. Donc pour la terre autour de 40 000 km, le 10 millionième du quart du méridien correspond à 1 m. A ne pas confondre avec la définition du méridien géographique qui a été établi après la première définition du mètre et qui est défini comme un demi-cercle, donc 20 000 km pour la terre.
Deux équipes pour la mesure de l’arc méridien
Dans l’équipe de Delambre se trouvent les français Lalande et Bellet ; Tranchot et Esteveny eux accompagnent Méchain. L’Académie des Sciences a réparti la mesure de l’arc du méridien de la façon suivante : les deux tiers supérieurs, de Dunkerque à Rodez, incombent à Delambre ; le dernier tiers, de Rodez à Barcelone, relève de Méchain. Cette disproportion se justifiait dans la mesure où le parcours de Delambre devait théoriquement repasser à peu près par les points de l’ancienne triangulation, tandis que Méchain s’aventurait sur un territoire vierge de toutes mesures géodésique.
En fait, les repères des triangulations antérieures se révéleront inutilisables : dans les troubles de la révolution des clochers ont disparu ou menacent de tomber en ruines. Sommet après sommet Delambre découvre que les anciens repères que Cassini avait utilisés sont inexploitables : les anciens clochers ayant été reconstruits d’une autre façon après incendie.
Jalonner l’arc méridien, une entreprise pleine de difficultés
Il fallut plus de cent triangles pour jalonner l’arc du méridien ; sur ce parcours nos deux géodésiens connurent bien des mésaventures : arrestations, révocations temporaires, ou encore endommagements et destructions de leurs ouvrages géodésiques. En effet, les signaux repères qu’ils utilisaient pour leurs observations excitaient la méfiance de la population ; les étoffes qui terminaient ces signaux étaient de couleurs blanche, or le blanc était la couleur de la royauté, donc une couleur contre révolutionnaire. Munis de laissez-passer, passeports, et autres autorisations, nos deux savants n’étaient cependant pas à l’abri des arrestations, car les institutions dont émanaient ces documents disparaissaient faisant d’eux des hors la loi. Ainsi, suite à la suppression des académies (en 1793), Delambre apprend son exclusion de la commission temporaire des poids et mesure (en 1794), il se voit interdit de poursuivre ses travaux, jusqu’en juin 1795. De son côté, Méchain connaît lui aussi bien des difficultés.
Aux repères à établir, aux montagnes à traverser se greffent les évènements historiques :
Une partie de ces mesures doit être réalisée sur le territoire espagnol tandis que la guerre entre la France et l’Espagne débute le 7 mars 1793. De 1793 à 1795, l’instauration de la Terreur va donc ralentir les travaux de la triangulation. Parallèlement, le mètre est provisoirement fixé par la loi du 1er août 1793 d’après les résultats de la mesure de la méridienne de France, publiés par Lacaille dans les Mémoires de l’Académie pour 1758. En outre, les subdivisions décimales du mètre seront le décimètre, le centimètre et le millimètre. Ce mètre étalon est temporaire, il ne correspond pas aux travaux de Méchain et Delambre, mais aux résultats de l’ancienne triangulation de Cassini.
1799, un nouveau mètre étalon en platine
En 1795, la situation politique s’améliorant, les travaux de la triangulation peuvent reprendre ; ils se poursuivront durant encore trois ans, avant que la longueur du quart du méridien puisse être précisément déterminée, et qu’un nouveau mètre-étalon en platine, dédié " à tous les temps, à tous les peuples ", ne soit déposé en 1799, aux archives de la république.
*photos extraites de l'ouvrage "L'épopée du mètre" (par Louis MARQUET et Albert LE BOUCH, publié par le ministère de l'industrie et de l'aménagement du territoire)
Le SI depuis mai 2019
Depuis son adoption par la CGPM en 1960, le SI a été révisé à plusieurs reprises. Cependant, la révision votée en 2018 et entrée en vigueur en mai 2019 présente ceci d'exceptionnel qu'elle modifie formellement toutes les définitions des unités en une seule fois, en révisant, qui plus est, de manière fondamentale, quatre d'entre elles. L'ampleur de cette révision est telle qu'elle a nécessité de nombreuses collaborations à l'échelle internationale entre de nombreux métrologues et scientifiques dans les champs les plus divers de la science.
2018 : changement de paradigme
La révision de 2018 constitue une évolution majeure du Système international d’unités (SI) tout en préservant bien sûr, l’ensemble des unités de mesure : les mêmes 7 unités de base associées aux 7 mêmes grandeurs de base ; les unités dérivées et les préfixes d’ores et déjà répertoriés ne s’en trouvent pas modifiés.
Il s’agit cependant d’une évolution conséquente et fondamentale pour les scientifiques : le socle sur lequel sont construites toutes ces unités est bouleversé. Dans un contexte industriel et médical où les mesures nécessitent une plus grande exigence (niveau d’incertitude, croisement de données de différentes grandeurs, moyens technologiques de plus en plus performants,…), il apparaît essentiel de rendre le SI encore plus cohérent qu’il ne l’est déjà. Trois raisons majeures peuvent être évoquées aisément pour étayer cette argumentation : la variation constatée sur un siècle de la valeur numérique du kilogramme étalon (prototype international du kilogramme - IPK); l’impossibilité de réaliser en pratique la définition de l’ampère ; l’indépendance des définitions entre la plupart d’entre elles.
Le principe de base de la révision du SI est de le fonder, non plus sur les unités elles-mêmes, mais sur 7 constantes de la physique : c’est le changement de paradigme de 2018. Ces constantes, que l’on appellera donc constantes de définition du SI reposent sur des phénomènes physiques de nature fondamentale, universelle (telles que h, la constante de Planck) ou sont dérivées de propriétés spécifiques (telle que l’efficacité lumineuse de l’œil). S’appuyer sur un socle de données « fixes » qui permet de bâtir le nouveau système est donc la garantie de travailler avec des mesures cohérentes dont on peut plus facilement repousser les limites (en théorie).
Les valeurs de ces constantes ont, pour quatre d’entre elles (Planck, Boltzmann, Avogadro, charge élémentaire), nécessité un travail de longue haleine à l’échelle internationale. La métrologie nécessite de la redondance pour valider de tels changements. De multiples expérimentations ont été mises en place afin d’en figer les valeurs numériques, admises par la communauté internationale. La convergence des résultats (assurée par plusieurs conditions définies au préalable lors du lancement de ces études par le Comité Consultatif des Unités sous l’égide du BIPM), a abouti en juillet 2017 à un ensemble de valeurs numériques entérinées par CODATA et récapitulés ci-dessous.
| Nom | Symbole | Valeur numérique | Unité |
|---|---|---|---|
| Constante de Planck | h | 6,626 070 15 × 10-34 | J∙s |
| Charge élémentaire | e | 1,602 176 634 × 10-19 | C |
| Constante de Boltzmann | k | 1,380 649 × 10-23 | J∙K-1 |
| Constante d’Avogadro | NA | 6,022 140 76 × 1023 | mol-1 |
Référence : “The CODATA 2017 values of h, e, k, and NA for the revision of the SI", D B Newell1, F Cabiati, J Fischer, K Fujii, S G Karshenboim, H S Margolis, E de Mirandés, P J Mohr, F Nez, K Pachucki, 29 January 2018, Metrologia, Volume 55, Number 1
Contributions françaises
Lors de la 21ème Conférence Générale des Poids et Mesures, en 1999, la recommandation suivante a été actée par les Etats membres : « … que les laboratoires nationaux poursuivent leurs efforts pour affiner les expériences qui relient l'unité de masse à des constantes fondamentales ou atomiques et qui pourraient, dans l'avenir, servir de base à une nouvelle définition du kilogramme…».
Plusieurs laboratoires nationaux de métrologie ont ainsi orienté leurs efforts vers une amélioration de l'incertitude de la valeur de constantes fondamentales et lancé des expériences de réalisation des unités, en particulier pour les unités relatives à la masse, l'électricité, la température et la quantité de matière.
Le réseau français de métrologie a donc démarré, dans les années qui ont suivis cette recommandation, plusieurs projets de recherche permettant à la France d'être au premier rang pour cette nouvelle redéfinition du SI. Nos travaux nationaux se sont donc concentrés sur les axes suivants.
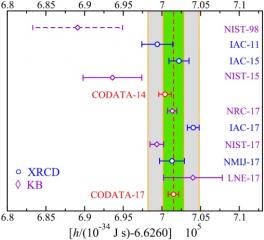
Le kilogramme et la constante de Planck, h.
La balance de Kibble (autrefois appelé « balance du watt ») est une instrumentation qui permet de comparer, dans deux configurations (dites statique et dynamique) deux types d’énergie : l’une électrique, dont la quantification élémentaire est la constante de Planck ; l’autre mécanique, de nature potentielle et reliée à la masse de l’objet que l’on compare.
Les équipes françaises se sont donc lancées en 2002 dans un projet de grande envergure, pour concevoir et réaliser cette instrumentation, impliquant des chercheurs du Cnam, du LNE et de l'Observatoire de Paris. Chaque équipe apportant son expertise sur les domaines scientifiques primordiaux de l’expérience : masse, électricité et magnétisme et enfin, gravimétrie. L’objectif était dans un premier temps (à échéance de juillet 2017) de contribuer à la détermination internationale de la valeur de h avec une incertitude cible de 8 x 10-8. Quatre valeurs de h ont été successivement publiées par la France entre 2014 et 2017. Le laboratoire se positionne aujourd’hui parmi les laboratoires internationaux (avec le NRC - Canada, le NIST - Etats-Unis ) qui ont contribué à la détermination actuelle de cette constante fondamentale, par l’expérience de balance de Kibble. L’objectif est aujourd’hui de réaliser la chaîne de dissémination du kilogramme en France, conformément aux missions de nos laboratoires nationaux. Des travaux ont, du reste, déjà été menés, dans le cadre du projet européen NewKilo pour évaluer l’utilisation de plusieurs matériaux comme étalon de transfert potentiel. Les études ont porté plus spécifiquement sur la physico-chimie de surface d’artefacts de différentes compositions. L’iridium semble être un bon candidat car il possède une faible susceptibilité magnétique (≃ +3.7 x 10-5) et une dureté élevée (≃ 450 Hv).
Référence : “Data and analysis for the CODATA 2017 special fundamental constants adjustment*” Peter J Mohr, David B Newell, Barry N Taylor and Eite Tiesinga,
Metrologia, Volume 55, Number 1
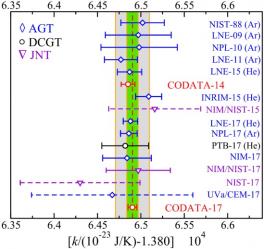
Le kelvin, via la détermination de la constante de Boltzmann, k
Deux méthodes ont été explorées par les laboratoires français. La méthode spectroscopique par le Laboratoire de Physique des Lasers et la méthode acoustique par le Laboratoire commun de métrologie.
Le LNE-LCM a publié 4 valeurs de la constante de Boltzmann, dont la dernière, en 2017 est le meilleur résultat obtenu à l’échelle internationale : 1,380 648 78 J·K-1 avec une incertitude inférieure à 6 x 10-7.
Référence : “Data and analysis for the CODATA 2017 special fundamental constants adjustment*” Peter J Mohr, David B Newell, Barry N Taylor and Eite Tiesinga,
Metrologia, Volume 55,Number 1
La traçabilité à l’ampère
Jusqu'à la révision de sa définition en 2018, la réalisation stricto-sensus de l’ampère n’était pas faite, sa définition la rendant irréalisable (conducteurs infinis, de sections négligeables, dans le vide…). La réalisation pouvait se faire via le farad, l'ohm et le volt. Les découvertes de l'effet Hall quantique et de l'effet Josephson, respectivement pour les mesures de résistances et de tensions, ont révolutionné la métrologie électrique. Des étalons électriques ont été mis en œuvre, depuis de nombreuses années, utilisant ces dispositifs quantiques, et déjà liés aux constantes fondamentales e et h. Toutefois, l'universalité de ces phénomènes devait être prouvée. Pour rendre sa cohérence au système, les équipes du LNE ont travaillé à cette nouvelle définition, en étudiant la détermination directe de la constante de von Klitzing (RK) par la réalisation d’un nouvel étalon calculable de Thompson-Lampard à cinq électrodes. Ces développements ont ainsi permis de démontrer la faisabilité de l’opération. Le développement de cette instrumentation se poursuit aujourd’hui dans le cadre de la mise en place d’une chaîne de comparaisons d’impédances performante : cet ensemble permettra une détermination directe du farad, puis de l’ohm en unités SI.
Par ailleurs, la mise en pratique de la nouvelle définition de l’ampère pourra être réalisée en utilisant un étalon quantique de courant. Les équipes françaises poursuivent actuellement leurs développement d’une source quantique de courant électrique (entre 10 pA et 100 pA) avec une exactitude de l’ordre de 10–7 en valeur relative. Ce fut également l’objectif du projet européen EMRP Qu-Ampere, achevé en avril 2015 et auquel le LNE a contribué en étudiant de nouvelles pompes à électrons et en développant un nouveau comparateur cryogénique de courants (CCC).
Perspectives pour le SI
Redéfinition de la seconde
Les instances internationales envisagent d’ores et déjà de futures améliorations aux définitions du SI, en particulier pour la candela et la seconde. Aujourd’hui, la seconde est définie à partir d'horloges atomiques à atomes de césium qui opèrent à des fréquences micro-ondes (autour de 9 GHz). Les recherches scientifiques ont démontré que plus on montait en fréquence, plus on arrivait à diminuer l'incertitude de mesure sur la fréquence. L’étape suivante, pour la réalisation de l'unité de temps, est l'amélioration de l'exactitude par les développements très prometteurs d'horloges, cette fois-ci dans le domaine des fréquences optiques (quelques centaines de THz), horloges à atomes neutres ou à ions. La France, pour sa part, développe deux types d'horloges à atomes neutres de Sr et de Hg. De telles expériences devraient améliorer de plus d'un ordre de grandeur la définition de la seconde.
Numérisation de la métrologie
La transformation numérique de la métrologie fait référence à l'adoption et à l'intégration des technologies numériques dans les processus de mesure. Elle a des impacts significatifs sur l'avenir de la métrologie, en transformant la façon dont les mesures sont effectuées et en facilitant l'échange et la gestion des données.
Nous pouvons lister quelques-uns des impacts clés de la transformation numérique de la métrologie :
1. Automatisation des processus de mesure : Les technologies numériques permettent d'automatiser les processus, réduisant ainsi la dépendance à l'égard de l'intervention humaine et minimisant les erreurs potentielles. Cela permet d'améliorer la reproductibilité et la précision des mesures, ainsi que d'accroître l'efficacité des opérations liées au processus de mesure.
2. Capteurs intelligents et Internet des objets (IoT) : Les capteurs intelligents connectés en réseaux jouent un rôle clé dans la transformation numérique de la métrologie. Ces capteurs sont capables de recueillir des données de mesure en temps réel, de les transmettre à des systèmes informatiques centraux et de les analyser automatiquement. Cela permet une surveillance continue et en temps réel des grandeurs mesurées, améliorant ainsi la réactivité et la gestion des processus de mesure.
3. Analyse des données et apprentissage automatique : ces évolutions de la métrologie tendent vers l'exploitation de vaste quantités de données de mesure générées. Les techniques d'analyse des données et d'apprentissage automatique peuvent être utilisées pour extraire des informations pertinentes à partir de ces données, identifier des modèles, détecter des anomalies et améliorer les performances de mesure. Cela ouvre la voie à une métrologie plus prédictive et proactive.
4. Intégration des systèmes de gestion de la qualité : Les technologies numériques facilitent l'intégration des systèmes de gestion de la qualité avec les processus de métrologie. Les données de mesure peuvent être directement intégrées dans les systèmes de gestion de la qualité, ce qui renforce la traçabilité et l'assurance qualité des produits et services. Cela permet également une gestion plus efficace des certificats d'étalonnage, des normes de référence et des procédures de contrôle qualité.
5. Interconnexion et échange de données : Les technologies numériques facilitent l'échange et le partage de données de mesure entre différentes parties prenantes, telles que les laboratoires de métrologie, les fabricants, les organismes de réglementation, etc. Cela favorise la collaboration, la transparence et l'interopérabilité entre les différents acteurs du secteur, ce qui contribue à l'amélioration globale de la qualité des mesures.
En résumé, la transformation numérique de la métrologie révolutionne les pratiques traditionnelles de mesure en intégrant des technologies numériques avancées. Cela conduit à une métrologie plus automatisée, précise, prédictive et intégrée, avec des impacts significatifs sur l'amélioration de la qualité des mesures, la productivité des processus et la prise de décision basée sur des données de mesure fiables.